Mastering Queue Data Structure in C++: A Comprehensive Guide
Complete Guide to Queue in C++
A queue is an important Data Structure with real-world usage. It is similar to a Stack but different in terms of implementation and application. This blog will introduce you to queue, its logical representation as an abstract data type and its implementation using arrays and linked lists. We will also see the basic operations that we can perform on Queue in C++ and its applications.
Queue
A queue at its core is just a list of a particular type of Data Objects or elements. Just like a Stack, a queue also follows a certain order in which the operations are performed on its data elements.
This order is known as First In First Out (FIFO). An example of a queue can be a line of people in a Bank Atm. A person who comes first and joins the line of people is able to withdraw their money first.
Queues vs Stacks
| Stacks | Queues |
| Stacks follow the principle of LIFO i.e., Last in First Out. The element to be inserted last is also the first to come out of the List. | Queues follow the principle of FIFO i.e., First in First Out. The element to be inserted first is also the first to come out of the List. |
| We insert and delete elements from the same end in a Stack. | We insert elements from the rear and delete them from the front end in a Queue. |
| Inserting an element is called a Push operation | Inserting an element is called enqueue operation. |
| Deleting an element is called a Pop operation. | Deleting an element is called a dequeue operation. |
| We use one pointer to represent and maintain the Stack known as the Top. It points to the last element inserted in the List. | We use two pointers to maintain the Queue. A front pointer points to the first element inserted in the List and a rear pointer points to the last element inserted in the List. |
| Stack doesn’t have any types. | The queue has 3 types namely: circular queue, priority queue and double-ended queue. |
Queue as ADT
In the real world, any structure in which what goes first comes out first is a queue. In short, we call queue a First in First out (FIFO) structure. unlike Stack, insertion and deletion happen from two different ends.

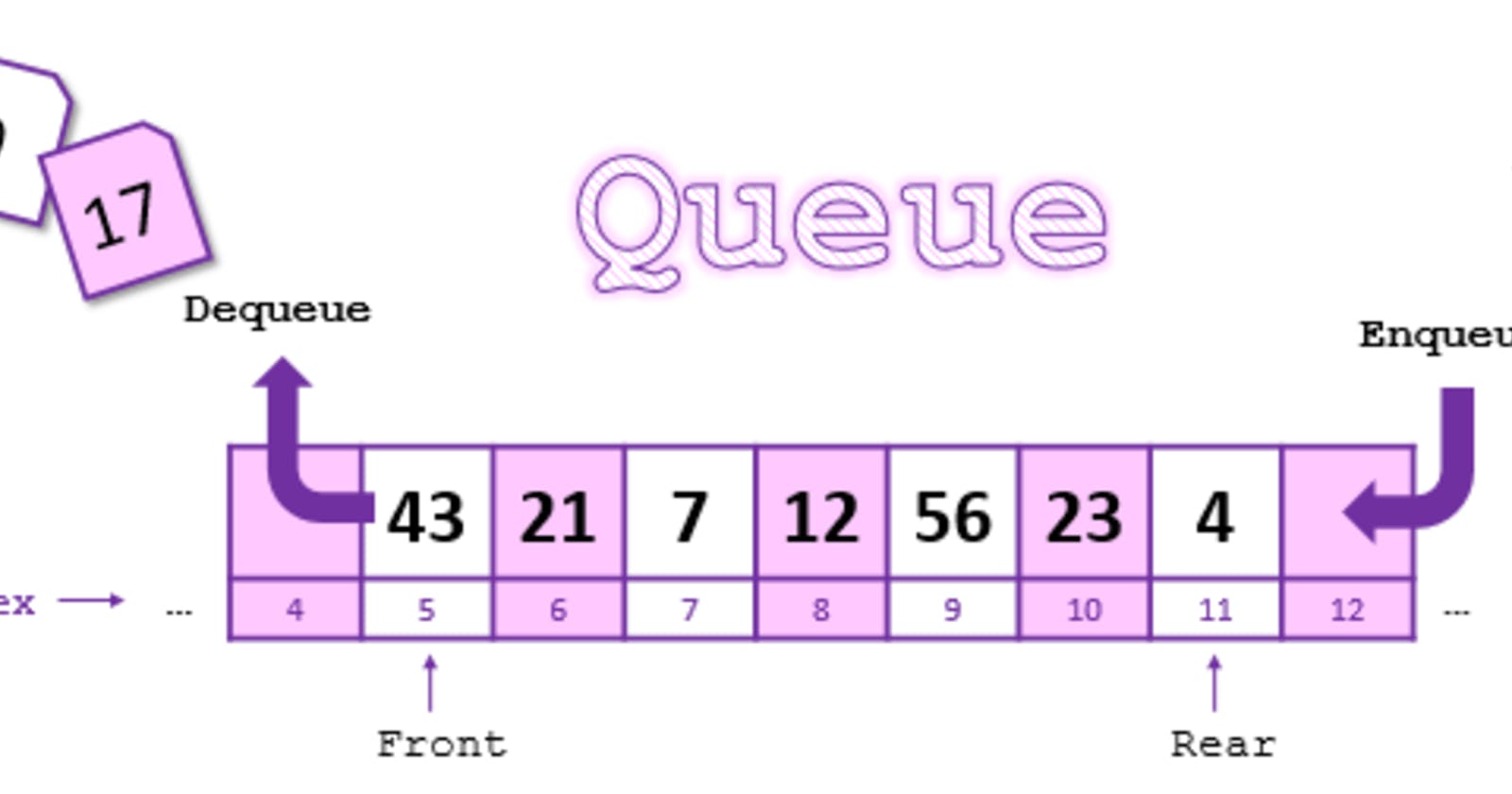
Insertion happens from the tail of the queue known as the rear. Deletion happens from the head of the queue known as the front.
Formally, we can define a queue as a list or collection with the restriction or the constraint that insertion can be and must be performed at one end (rear). Not only that, deletion can be performed at another end (front) of the queue.
The Queue Interface
Just like a Stack, a queue has two fundamental operations:
Enqueue(x): This operation inserts an element into the queue. Here x will be passed to enqueue function and then added to the List.
Dequeue(): This operation deletes an element from the queue. Typically a dequeue function also returns the removed element.
void Enqueue(int abc);
int Dequeue();
Enqueue is returning void here while Dequeue is returning an integer. This integer should be the removed element from the queue. But you can also design a dequeue operation to return void.
There are a few other basic operations too:
peek(): This operation returns the element at the head. we can also name it front(). It is similar to the top() operation we have in the stack.
isEmpty(): It checks if the queue is empty or not and returns a boolean answer i.e., true if it is and false if it is not.
isFull(): it checks if the queue is full or not and returns a boolean answer i.e., true if it is and false if it is not.
All the operations above must take constant time. the time complexity of each operation is O(1).
Logically a Queue can be shown as a figure or container open from two sides. On one side to enqueue or insert an element and another side to dequeue or delete an element.

Let’s take a practical example to understand how Queue works. Suppose we have a network of computers with a few printers to print documents of all the connected systems.
A printer can only print one document at a time and rejecting the print request from a computer while it is printing something is inefficient.
So the printer queue up all the print requests and print document in the order of First in First Out.

Applications of Queue
A Queue is most often used in a scenario when there is a shared resource that is supposed to serve some request but the resource can handle only one request at a time. In such a case, we queue up all the requests. The request that comes first gets served first
Some well-known applications of the queue are as follows:
A single shared resource (CPU, Disk, and Printer) uses Queue to maintain a waiting List.
Music Playlists use queues to create a List of Songs and play them in the order we want.
In messaging apps, our messages are queued and sent according to the order in which they were sent.
Process Scheduling and simulating Wait.
The queue is extensively useful in Operating systems and networks for buffering, spooling, memory management etc.
Queue Simulation in a Printer
As the above text already states Queue follows the principle of first-in-first-out (FIFO). This of it by an example of a person standing in line at the ticket counter. The self-explanatory rule is that the person who enters the line first must avail of the benefit of it by buying the ticket first.
Queue works in a similar fashion. If there are multiple tasks we want to do then Queue will list and perform them in order of their arrival. This means that the task to come first will also be the first one to get executed.
Printers work in the same way.

In the above example, a printer is in connection with multiple computers at the same time. Any request to print anything from any of the three computers will be completed by the same Printer.
Suppose each of the computers made some requests at different points in time. Let’s name them Job1, Job2 and Job3.
Job1 – Print my Invoice
Job2 – Print my CV
Job3 – Print form X
As soon as the printer receives all the print requests, it uses a Queue to list them in order of Job arrival. It serves the requests on a first come first serve basis.
Breadth First Search Algorithm
One of the applications of Queue is the BFS. Breadth First Search and the BFS algorithm is basically a searching algorithm. It involves a series of sequential steps that helps us find a specific node in a Tree or a Graph. While traversing through the nodes, if any one of them meets the criteria we provide beforehand is retrieved, and we then use it accordingly.
Although the implementation of BFS in the case of both graphs and trees is the same, there happens to be a slight difference. Unlike Graphs, there is a possibility of repeated nodes in the graph and that is why to avoid these cycles, we divide the respective vertices into two categories: visited and not-visited.
To track all the vertices that we visit, we use an array that stores boolean values. Meanwhile, a Queue is used for traversing through the data structure.
Array implementation of Queue
So we are saying that a Queue is a special kind of List in which the insertion and deletion happen one at a time and from different ends.
Let’s take an array of 10 integers. This array will contain our queue.

At any point, some part of the array starting at the index marked as the front, till an index marked as rear will be my Queue. We will add elements from the rear and delete elements from the front.

To add an element to the queue we can increment the rear and write a new value. Let’s add 5 to the existing Queue.

Now let’s remove an element from the Queue. In this particular example, we have to remove 2 from the Queue. To do that we can simply increment the front because at any point only the cells starting from front to rear are part of my queue. By incrementing the front, we are discarding 2 from the queue.

Now let’s write the pseudo-code for the above implementation.
int array[10];
front = -1;
rear = -1;
// Function to check if queue is Empty
isQueueEmpty(){
if (front == -1 && rear == -1){
return true;
}else{
return false;
}
}
// Function to insert an element in the queue
enqueueElement(element){
// If array is Full then function call ends here
if (rear == size(array)-1){
cout<<"Array is completely filled";
return;
}
// if queue is empty then we set front and rear to 0
else if(isQueueEmpty()){
front = 0;
rear = 0;
array[rear] = element;
}
// if queue is not empty then simply incremnent rear by 1
else{
rear = rear + 1;
array[rear] = element;
}
}
// Function to delete an element from the Queue
dequeueElement(element){
// If queue is empty then, function call ends here
if(isQueueEmpty()){
return;
}
//If queue has one element only:
else if (front == rear){
front = -1;
rear = -1;
}
else{
front = front + 1;
}
}
let’s enqueue 3 elements into the Queue.
enqueueElement(2);
enqueueElement(5);
enqueueElement(7);

Let’s now perform a dequeue operation and remove 2 as it is at the front of the queue.

Limitation of Array Implementation: If the array is full and then we want to insert a new element into the queue we’ll have to either deny the request or create a new array of larger size and copy all the elements of the existing queue into this new array. This process is costly and hence inefficient.
Another problem could be that we have a large enough array and too few elements. In such a case the memory lest to fill is a waste.
Linked List Implementation of Queue
A Linked List as we know is a collection of entities that we call nodes, and these nodes are stored at non-contiguous locations in memory. Each node contains two fields, one to store data and another to store the address of the next node.

In the normal implementation of Linked List, if we insert at one side and remove from another side then one of these operations enqueue or dequeue, depending on how we pick the side will cost us O(N), but the requirement we have is that both these operations should take constant time.
We can do this by adding an additional pointer along with a head that points to the last node of the queue. This way we don’t need to traverse the Linked List every time if we want to insert an element.

Let’s see how we can implement this interface using Linked List in C++.
#include<bits/stdc++.h>
using namespace std;
// A Linked List Node Structure
struct Node{
int data_Element;
struct Node* next_Node;
};
// front: Points to First Node of List
struct Node* front_Node = NULL;
// Rear: Points to Last Node of List
struct Node* rear_Node = NULL;
// Function to add new element to Queue
void enqueueElement(int element){
Node* temp = new Node();
temp->data_Element = element;
temp->next_Node = NULL;
if (front_Node == NULL && rear_Node == NULL){
front_Node = rear_Node = temp;
return;
}
rear_Node -> next_Node = temp;
rear_Node = temp;
}
// Function to delete element from Queue
void dequeueElement(){
Node* temp = front_Node;
if (front_Node == NULL){
cout<<"Queue is Empty\n";
return;
}
if (front_Node == rear_Node){
front_Node = rear_Node = NULL;
}else{
front_Node = front_Node -> next_Node;
}
free(temp);
}
// function to return the first element of Queue
int Front() {
if(front_Node == NULL) {
cout<<"Queue is empty\n";
return 0;
}
return front_Node->data_Element;
}
// function to print the entire Queue
void Print() {
struct Node* temp = front_Node;
cout<<"Queue: ";
while(temp != NULL) {
cout<<temp->data_Element<<" ";
temp = temp->next_Node;
}
cout<<"\n";
}
int main(){
cout<<"OUTPUT\n-----------------\n";
Front();
// Insert 7 in Queue
enqueueElement(7);
Print();
// Insert 24 in Queue
enqueueElement(24);
Print();
// Insert 69 in Queue
enqueueElement(69);
Print();
// Delete element from front
dequeueElement();
Print();
// Insert 11 in Queue
enqueueElement(11);
Print();
}

Circular Queue
The Circular Queue is very similar to the normal Queue. The only difference is that the last element is in connection to the first element of the List. This also follows the FIFO principle.
Circular Queue is beneficial because, in a regular Queue, we can not insert elements after the Queue is full. This creates a problem of memory waste and management. There could be enough space to insert data elements at the front but the rear may be posing as a completely full Queue.

Here is the C++ code to implement Circular Queue:
We can perform the following Operations on the Circular Queue:
enqueue – This method allows us to insert an element into the Queue. just like a regular queue, we insert a new element from the rear.
dequeue – This method allows us to delete an element from the Queue. The element is removed from the front of the Queue as per FIFO.
These are the primary operations of Circular Queue but we can create other operations to get the front and rear elements of Queue, check if Queue is empty or Full etc.
Here is the C++ code for Circular Queue Implementation.
#include <bits/stdc++.h>
using namespace std;
const int QUEUE_SIZE = 10;
// Class to define Circular Queue
class circularQueue {
public:
int data[QUEUE_SIZE];
int front; /// point to front of Queue
int rear; // point to rear of Queue
circularQueue() {
front = 0;
rear = 0;
}
// Function to check if Queue is Empty
bool isQueueEmpty() {
return front == rear;
}
// Function to check if Queue is Full
bool isQueueFull() {
return (rear + 1) % QUEUE_SIZE == front;
}
// Function to insert an element
void enqueueElement(int value) {
if (!isQueueFull()) {
data[rear] = value;
rear = (rear + 1) % QUEUE_SIZE;
} else {
cout << "Queue is full!" << endl;
}
}
// // Function to delete a element
void dequeueElement() {
if (!isQueueEmpty()) {
front = (front + 1) % QUEUE_SIZE;
} else {
cout << "Queue is empty!" << endl;
}
}
// Functio that returns the Front element of Queue
int frontElement() {
if (!isQueueEmpty()) {
return data[front];
} else {
cout << "Queue is empty!" << endl;
return -1;
}
}
};
// Main Function of the Program Starts
int main() {
circularQueue queue;
// Checking if the Queue is Empty
if (queue.isQueueEmpty()){
cout<<"Queue is Empty\n";
} else{
cout<<"Queue is not Empty\n";
}
// Insert element 7
queue.enqueueElement(7);
// Insert element 11
queue.enqueueElement(11);
// Insert element 23
queue.enqueueElement(23);
cout << queue.frontElement() << endl;
// Remove element from Rear
queue.dequeueElement();
cout << queue.frontElement() << endl;
// Remove element from Rear
queue.dequeueElement();
cout << queue.frontElement() << endl;
// Remove element from Rear
queue.dequeueElement();
// Checking is the Queue is Full
if (queue.isQueueFull()){
cout<<"Queue is Full\n";
} else{
cout<<"Queue is not Full\n";
}
return 0;
}
Output:

Double Ended Queue
The Double ended queue is also a type of List like regular and circular Queues. The only difference is that it allows us t to add or remove an element from both the front and rear sides.

#include<iostream>
using namespace std;
#define SIZE 10
// Class Dequeue to define Double Ended Queue
class Dequeue {
int array[20],front,rear;
public:
Dequeue();
void insertAtStart(int);
void insertAtEnd(int);
void deleteFront();
void deleteRear();
void show();
};
// Constructor to set initial front and rear
Dequeue::Dequeue() {
front = -1;
rear = -1;
}
// Function to insert element at end of Queue
void Dequeue::insertAtEnd(int i) {
if(rear >= SIZE-1) {
cout<<"\nQueue is Full!!";
} else {
if(front == -1) {
front++;
rear++;
} else {
rear += 1;
}
array[rear]=i;
cout<<"\nInserted item is: "<<array[rear];
}
}
// Function to insert element at start of Queue
void Dequeue::insertAtStart(int i) {
if(front == -1) {
front = 0;
array[++rear]=i;
cout<<"\ninserted element is: "<<i;
} else if(front != 0) {
array[--front]=i;
cout<<"\ninserted element is: "<<i;
} else {
cout<<"\nQueue is Full!!";
}
}
// Function to delete element at Start
void Dequeue::deleteFront() {
if(front == -1) {
cout<<"\nQueue is empty";
return;
}
else {
cout<<"\nThe Deleted element is:"<<array[front];
if(front == rear) {
front = rear = -1;
return;
} else
front += 1;
}
}
// Function to delete element at Rear
void Dequeue::deleteRear() {
if(front == -1) {
cout<<"\nDequeue is empty";
return;
}
else {
cout<<"\nThe Deleted element is:"<<array[rear];
if(front == rear) {
front = rear = -1;
} else
rear -= 1;
}
}
void Dequeue::show() {
if(front == -1) {
cout<<"\nDequeue is empty";
} else {
for(int i=front ;i<=rear ;i++) {
cout<<array[i]<<" ";
}
}
}
int main() {
Dequeue deque;
// Insert 11 at front
deque.insertAtStart(11);
// Insert 15 at End
deque.insertAtEnd(15);
cout<<"\n";
// Show Elements
deque.show();
// Delete Front Element
deque.deleteFront();
// Delete Rear Element
deque.deleteRear();
return 0;
}
Output:

Priority Queue
A Priority Queue is a Queue in which the first element is either the greatest element or the smallest. The rest of the List elements are either in increasing or decreasing order accordingly.
We can implement the priority queue in C++ using the Standard Template Library (STL). STL provides a ready-made implementation of Data Structures along with their basic operation functions.
C++ STL uses Priority Queue as an implementation Heap. The first element also known as the Top is the greatest element by default but we can also change it to the smallest.
Here is the C++ code to implement Priority Queue using the C++ STL.
#include <bits/stdc++.h>
#include <queue>
using namespace std;
// Main Function Starts
int main()
{
int array[10] = { 11, 4, 7, 13, 2, 8 , 23, 69, 33, -5 };
// Priority Queue SYNTAX
priority_queue<int> priorityQueue;
cout << endl;
// Inserting Array Elements into Priority Queue
for (int i = 0; i < 10; i++) {
// Push Element insert an element at the Top
priorityQueue.push(array[i]);
}
// Print elements of Priority Queue
cout << "Priority Queue is: ";
while (!priorityQueue.empty()) {
// top() Function gives element at the Top/Front of Queue
cout << priorityQueue.top() << ' ';
// pop() Function removes the element at the Top.
priorityQueue.pop();
}
return 0;
}
Output:

Conclusion
In conclusion, the queue data structure is very useful in computer programming. It allows for the efficient management of data by allowing us to add and remove items in a specific order. Implementing a queue in C++ is relatively straightforward using either an array or a linked list.
While there are various ways to implement a queue, the most important thing is understanding the principles behind its operation and how it can be used to solve problems. Whether you are a beginner or an experienced programmer, learning about the queue data structure is a valuable skill that will serve you well in your programming endeavours.